Tentukan interval x sehingga grafik f(x) = 2 sin (2x - 60°) cekung ke atas untuk 0° ≤ x ≤ 180°
Tentukan interval x sehingga grafik f(x) = 2 sin (2x - 60°) cekung ke atas untuk 0° ≤ x ≤ 180°!
Jawab:
f(x) = 2 sin (2x – 60°) cekung ke atas untuk 0° ≤ x ≤ 180°
Kita lakukan perhitungan seperti berikut:
Turunan pertama: f'(x) = 4 cos (2x – 60°)
Turunan kedua: f''(x) = –8 sin (2x – 60°)
Syarat kurva cekung ke atas:
f''(x) > 0
–8 sin (2x – 60°) > 0 ⇔ sin (2x – 60°) < 0
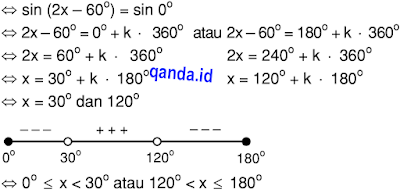
Pembuata nol:
sin (2x – 60°) = 0
Jadi fungsi f(x) = 2 sin (2x - 60°) cekung ke atas pada interval 0° ≤ x < 30° atau 120° < x ≤ 180°
-------------------------------------------
Mari Kita Selalu Belajar Bareng di
qanda.id
Jangan Lupa Komentar dan Saran di
nanangnurulhidayat@gmail.com
Posting Komentar untuk "Tentukan interval x sehingga grafik f(x) = 2 sin (2x - 60°) cekung ke atas untuk 0° ≤ x ≤ 180°"